Machine Learning Projects
Bayesian Optimization with Informative Covariance
Informative Covariance
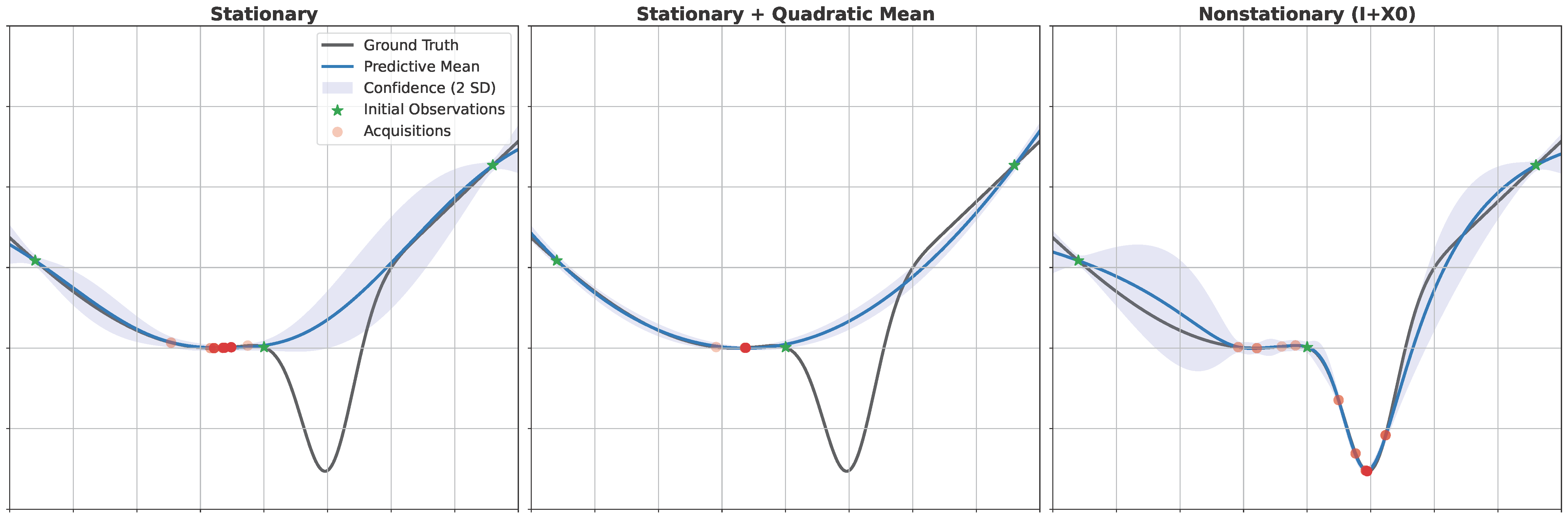
A class of informative priors over functions is proposed for optimization with Gaussian process surrogates. The proposed nonstationary covariance functions encode a priori preferences via spatially-varying prior (co)variances and promote local exploration via spatially-varying lengthscales. Both nonstationary effects are induced by a shaping function that captures information about the location of optima. Experiments show that these informative priors can significantly increase sample efficiency of high-dimensional Bayesian optimization, even under weak prior information. These priors also complement other methods, including trust-region optimization and belief-augmented acquisition functions.
(Mode-)Collapsed Acquisition Functions
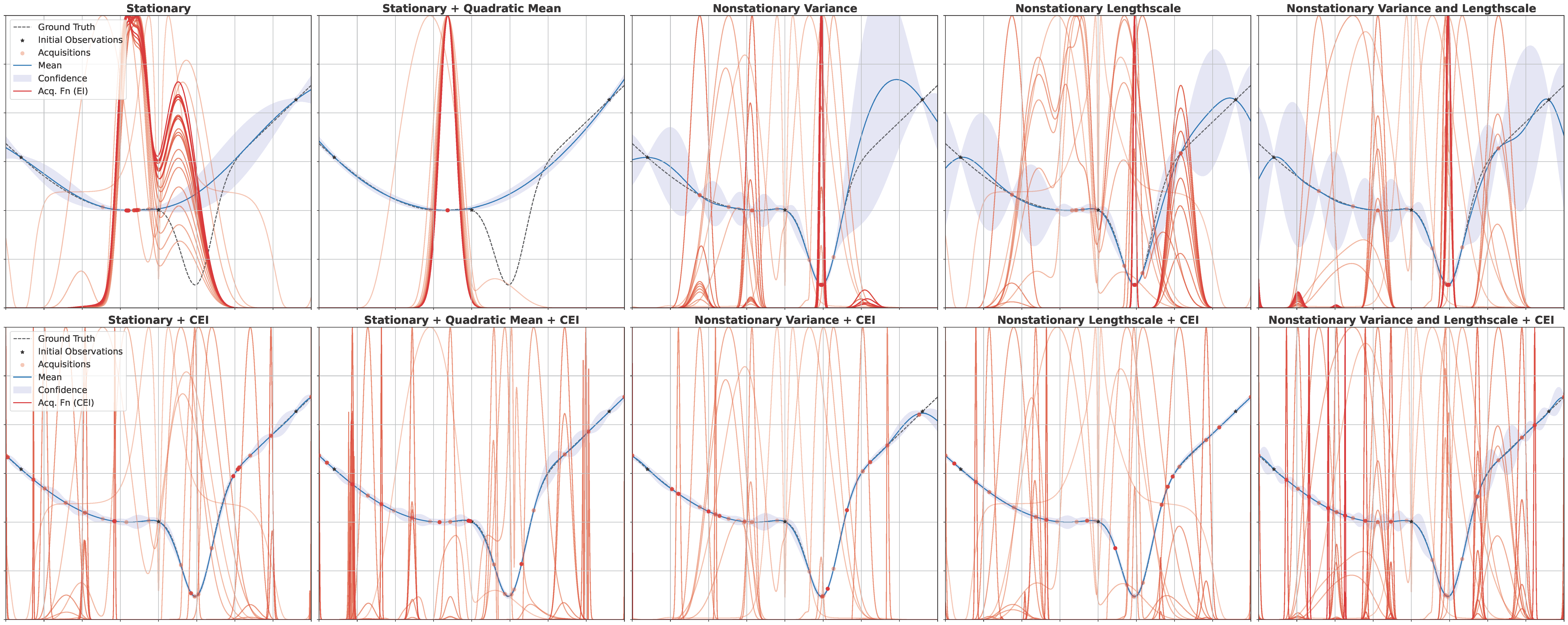
The problem above, that is due to overconfident stationary surrogates, can also be solved by modifying the acquisition step. The proposed Collapsed Expected Improvement (CEI) is based on the repeated application of the Laplace method with mode collapse, resulting in more informative acquisitions. This method may also be combined with informative priors. Since an approximate posterior over promising points is computed as a byproduct, this information may be used to update the shaping function that induces the nonstationary effects. In addition, the underlying idea offers a general strategy to estimate multimodal functions/distributions without the problems generally associated with 1-turn variational inference (mass-covering or mode-seeking).
High-dimensional Bayesian Optimization for Likelihood-Free Inference
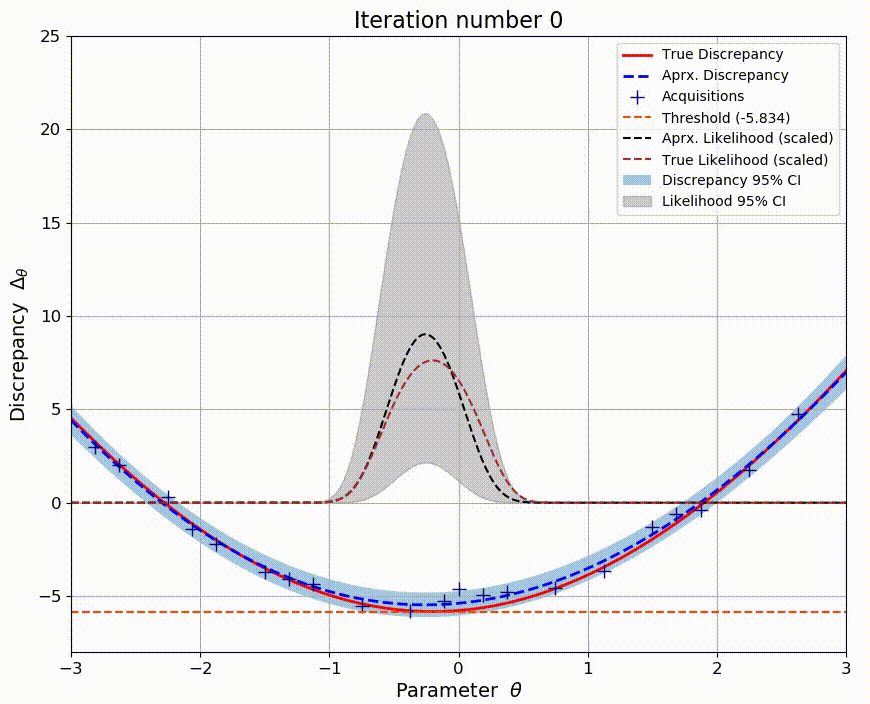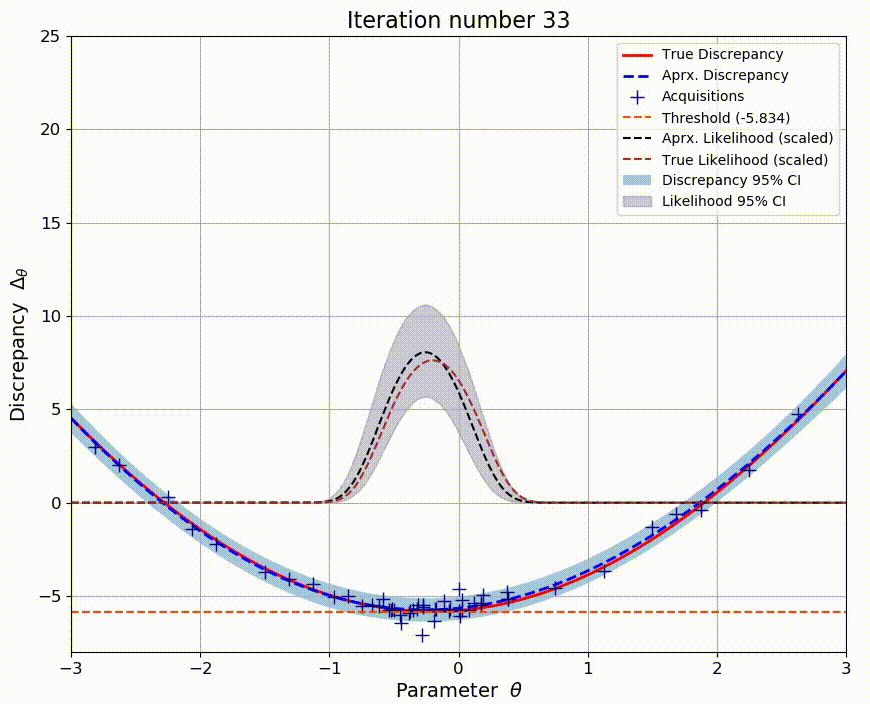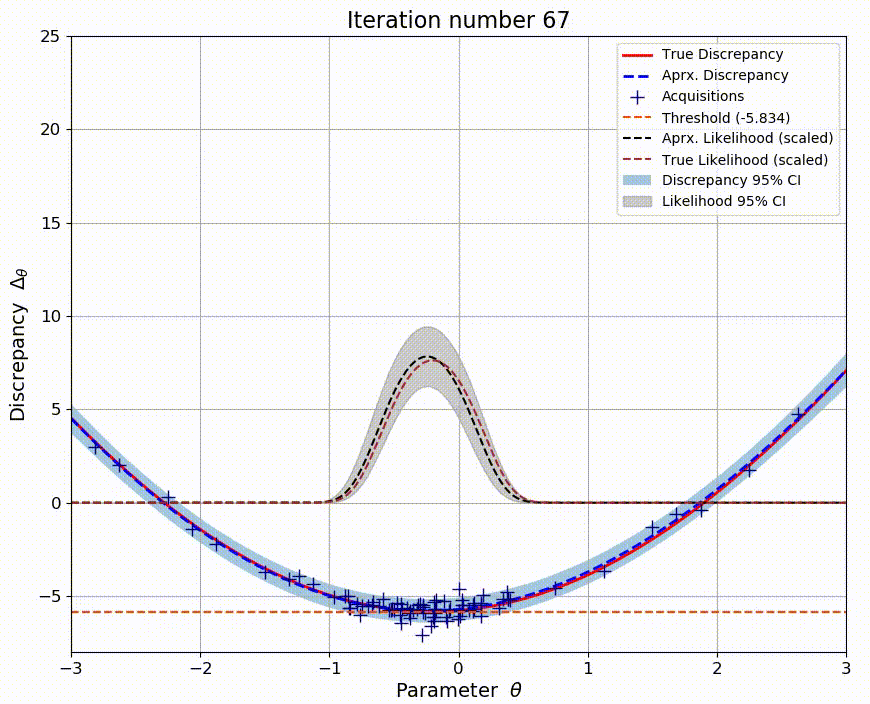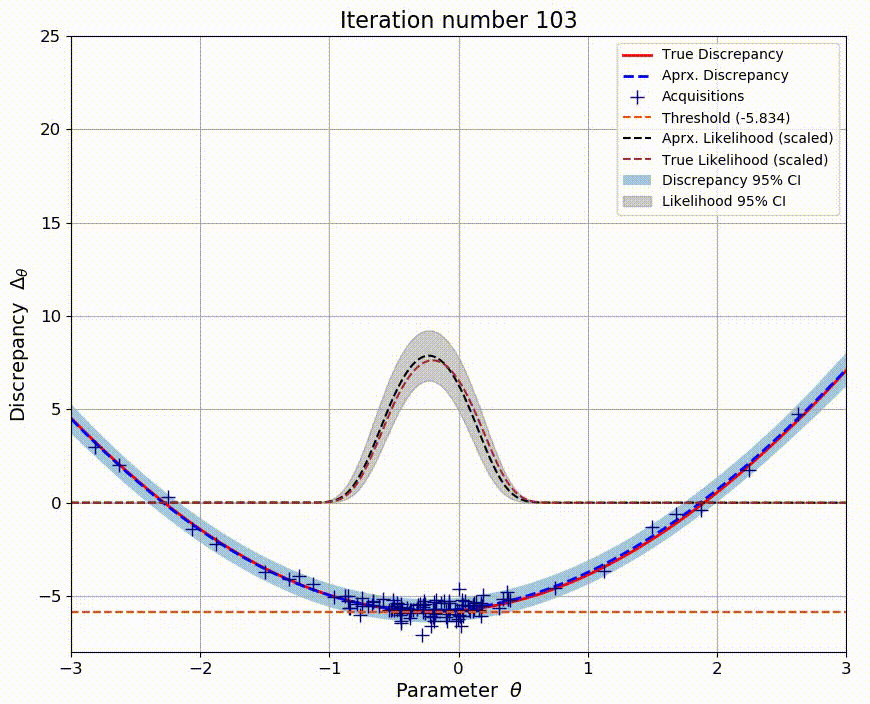
Standard inference methods rely on the ability to explicitly evaluate the likelihood function. However, many models such as those in natural sciences are based on stochastic simulators and the likelihood function is no longer available. Several likelihood-free inference methods attempt to solve this issue, but can be inefficient. As an alternative, Bayesian optimization for likelihood-free inference (BOLFI) has emerged. In this work, the focus is on relatively high-dimensional problems. By exploiting advances in high-dimensional Bayesian optimization with additive models, higher sample efficiency is possible. New performance measures are also designed and results demonstrate their usefulness.
Machine Learning Practical - Deep Learning
Report on Activation Functions Report on Learning rules, BatchNorm, and ConvNet
Interim Report on Neural Data Augmentation Report on Neural Data Augmentation
My interests in Bayesian statistics and machine learning led me to pursue a MSc in Artificial Intelligence at the University of Edinburgh, from which I graduated as the top student. Courses in Bayesian statistics were supplemented by more hands-on statistical programming and machine learning courses.
ECG-based Biometrics
Paper (2017) Poster (2017) Slides on ECG-based biometrics and dynamical systems (2017)

Biometric identification is the task of recognizing an individual using biological or behavioral traits. As a research assistant at IT-Lisbon, Pattern and Image Analysis, I collaborated on the Project LearnBIG, focusing on signal denoising and representations of physiological signals for biometric systems: 1) helped on the development and maintenance of databases to store and annotate biosignals; 2) explored deep learning architectures for ECG-based biometrics, finding that deep autoencoders successfully learn lower-dimensional representations of heartbeat templates, leading to superior identification performance, and that these can be learned offline; 3) implemented and tested other SOTA methods for feature extraction, dimensionality reduction and classification; 4) explored state-space models for statistical biosignal processing.
Pending Projects
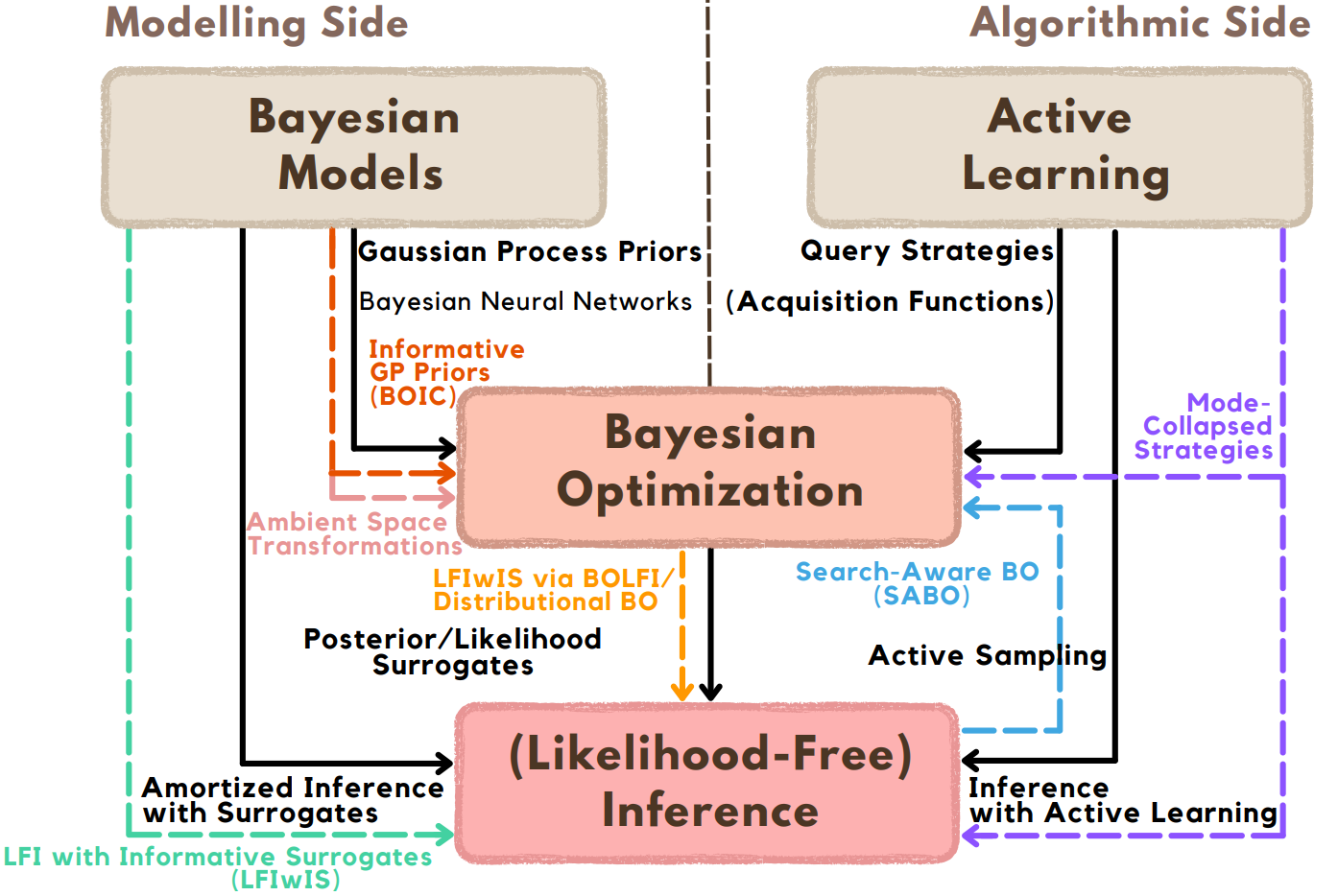
In order to develop more sample-efficient methods, BOIC focused on the design of more informative Gaussian Process (GP) priors for optimization (red), and the other objective is to accelerate Likelihood-Free Inference (orange). Another research direction focuses on ambient space transformations (pink), aiming to show that these transformations, including dimensionality reduction methods, are complementary to the proposed priors.
The exploration of active learning strategies, including ideas from Search-Aware Bayesian Optimization, is also a fruitful research direction.
Finally, there is the possibility to explore the connections between GP priors and Bayesian neural networks. It is typically more intuitive, and more model agnostic, to elicit priors in the observable/function space, rather than the space of neural network parameters, where there is a general lack of intrinsic meaning to experts, from which information is drawn.